Ángulos entre paralelas

Aprenda sobre los ángulos entre paralelas: enfoques de enseñanza

Hoy exploraremos un concepto divertido y práctico en geometría: los ángulos entre líneas paralelas. Nuestra misión es abordar este tema de una manera que sea comprensible y aplicable a nuestros estudiantes, utilizando una variedad de estrategias y herramientas.

Introducción a los ángulos formados por rectas paralelas y rectas transversales

Cuando una recta, que llamamos recta transversal, corta dos rectas paralelas, se forman ocho ángulos especiales. Estos ángulos tienen ciertas relaciones entre sí y el conocimiento de estas relaciones es crucial para resolver problemas geométricos. 

Primero, recordemos que dos rectas son paralelas si están en el mismo plano y nunca se cruzan, sin importar qué tan lejos se extiendan. Imaginemos que estamos observando que en la construcción de un techo plano de un edificio, vigas paralelas sostienen el techo y se cruzan con una viga transversal para reforzar la estructura.

Imaginemos que estamos construyendo un puente. Las vigas del puente son paralelas y deben estar adecuadamente sustentadas por otras estructuras. Aquí es donde entra en juego nuestra comprensión de los ángulos entre paralelas y transversales. Los ángulos con forma pueden ayudarnos a garantizar que todo esté en el ángulo correcto para lograr la máxima estabilidad y eficiencia.

Tipos de ángulos entre paralelas 

Definamos y examinemos los diferentes tipos de ángulos creados:

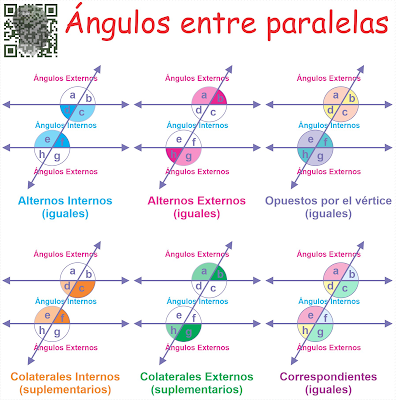
Ángulos correspondintes:  Estos ángulos están en la misma posición en cada intersección. Por ejemplo, si una transversal corta dos líneas paralelas, los ángulos en el mismo "ángulo" de cada intersección son los ángulos correspondientes. Estos ángulos son iguales (tienen la misma medida).

Ángulos alternos externos: estos ángulos se encuentran en lados opuestos de una línea transversal pero dentro de dos líneas paralelas. Al igual que los ángulos correspondientes, los ángulos alternos internos también son congruentes.

Ángulos alternos externos: se encuentran en lados opuestos de la línea transversal, pero fuera de los dos paralelos. Estos ángulos también son los mismos.

Ángulos colaterales internos (suplementarios): Son dos ángulos que están en el mismo lado de una línea transversal que cruza dos rectas paralelas, y se encuentran dentro de las dos rectas paralelas. Estos ángulos suman 180 grados.

Ángulos colaterales externos (suplementarios) Los ángulos colaterales externos son dos ángulos que están en el mismo lado de una línea transversal que cruza dos rectas paralelas, pero se encuentran fuera de las dos rectas paralelas. Estos ángulos suman 180 grados.

Ángulos correspondientes: Los ángulos correspondientes son dos ángulos que están en el mismo lado de una línea transversal que cruza dos rectas paralelas, ocupando la misma posición relativa en cada intersección. Estos ángulos son iguales en medida.

Cómo calcular un angulo entre dos rectar y una transversal

Juegos en Línea:

Utilicemos juegos como Transum - Angles in Parallel Lines para reforzar el aprendizaje de una manera lúdica e interactiva.

Otra herramienta útil es IXL - Parallel Lines Cut by a Transversal que ofrece ejercicios interactivos para practicar la identificación y cálculo de ángulos. 

Comprender los ángulos formados por líneas paralelas y líneas transversales es un paso importante para dominar la geometría. Al abordar este tema con una combinación de teoría, práctica visual y aplicación práctica, preparamos a nuestros estudiantes para aplicar eficazmente estos conceptos en situaciones del mundo real. A medida que avancemos, recordemos que la claridad y relevancia de nuestras explicaciones transformarán estos conceptos abstractos en herramientas prácticas y útiles para nuestros estudiantes.