Comenzando con Ángulos y Rectas
Hoy veremos ángulos y rectas, una parte fundamental de la geometría que es esencial para los estudiantes. Comprender estos conceptos no sólo es importante para la geometría, sino que también es la base de muchas aplicaciones en ciencia, ingeniería y diseño. Nuestro trabajo es aclarar estos conceptos y desglosarlos de manera que sean accesibles y relevantes para los estudiantes. A continuación, analizamos enfoques eficaces para enseñar estos temas en el aula.
Conceptualización
de líneas
Comience
explorando líneas. Es importante que los estudiantes comprendan la diferencia
entre rectas, segmentos de recta y rayos. La línea se extiende infinitamente en
ambas direcciones y no tiene espesor. Para concretar este concepto, utilice
ejemplos ambientales como las vías del tren y el horizonte. He de sugerir que
pienses siguiendo los lineamientos de tu vida diaria te ayudará a comprender
este concepto.
Utilice
herramientas digitales como GeoGebra y Desmos para facilitar una comprensión
más profunda. Estos permiten a los estudiantes interactuar y visualizar líneas.
Estos recursos no sólo hacen que la geometría sea más accesible, sino que
también mejoran la participación de los estudiantes al permitirles experimentar
con conceptos abstractos en un entorno visual.
Distinguir
y clasificar rectas
Introduzcamos
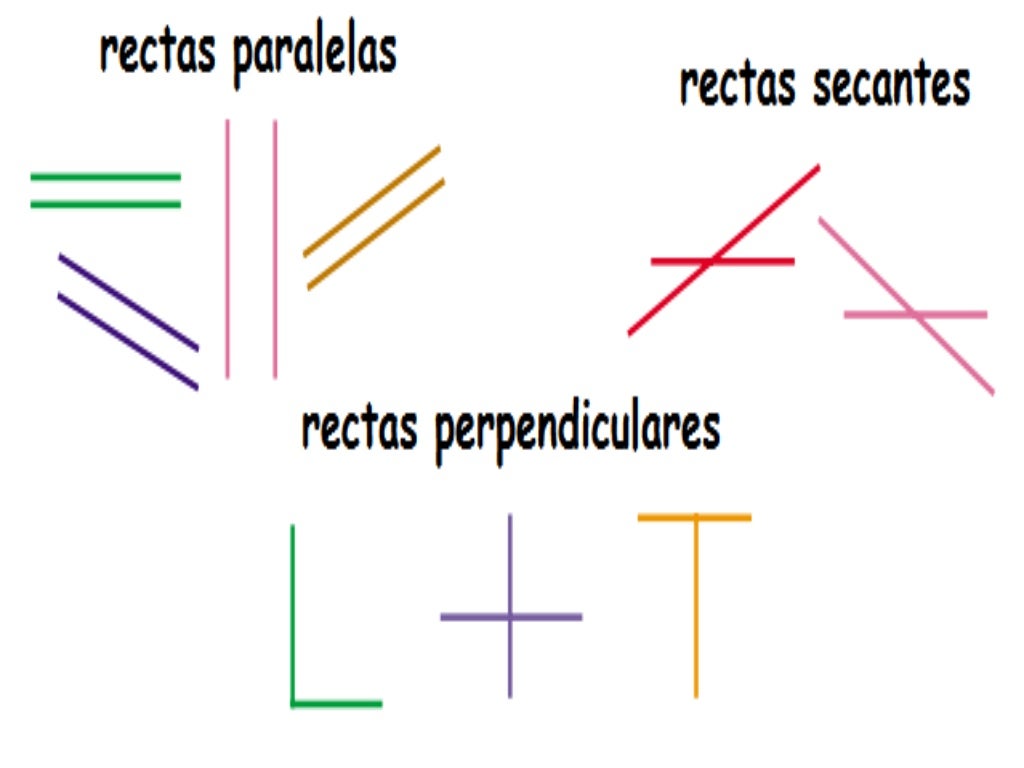
los diferentes tipos de rectas:
Rectas paralelas: Nunca se cruzan. Para explicar este concepto, usemos analogías como las vías del tren y los carriles de la autopista.
Líneas
Perpendiculares: se cruzan en ángulo recto (90 grados). Las intersecciones de la red
de carreteras son un gran ejemplo visual.
Sugerir
actividades prácticas como dibujar líneas paralelas y perpendiculares en papel
cuadriculado puede reforzar estos conceptos. Las líneas también se
pueden utilizar para ejercicios interactivos.
Presentamos
el ángulo
Ahora,
entremos en la historia del ángulo. Cuando dos líneas se cruzan, crean un
ángulo y la medida del ángulo indica la rotación de una línea con respecto a la
otra. Comprender los ángulos es esencial para estudiar formas geométricas y
resolver problemas del mundo real.
Para
enseñar este concepto, pida a los estudiantes que se imaginen abriendo un
libro. Un buen ejemplo es el ángulo que se forma entre las tapas de un libro.
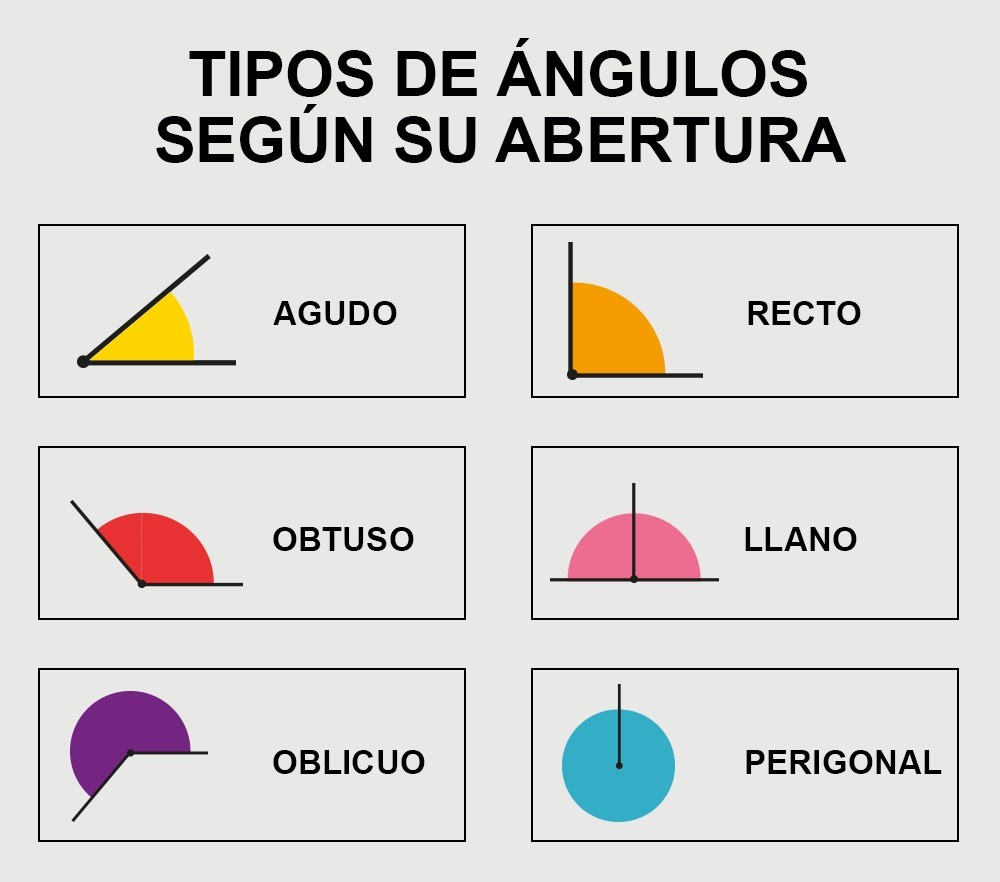
Es importante recalcar que los ángulos se miden en grados y explicar la
diferencia entre ángulos agudos, rectos, obtusos y rectos.
Ángulo
recto: Exactamente 90 grados, como una esquina de papel.
Ángulo
obtuso: mayor de 90 grados y menor de 180 grados, ej.: B. Apertura de una
puerta parcialmente abierta.
Ángulo
lineal: exactamente 180 grados como el horizonte.
Enseñanza
de la medición de ángulos
Enseñe
a los estudiantes cómo usar un transportador para medir ángulos. Aprenda
ejercicios prácticos para medir ángulos en diversas formas geométricas y
objetos cotidianos. Puede utilizar aplicaciones como Khan Academy, que
proporciona ejercicios interactivos sobre cómo medir ángulos.
Aplicaciones
Prácticas y Proyectos
Es
importante combinar teoría y aplicación práctica. Por ejemplo, puede pedirles a
los estudiantes que identifiquen ángulos en estructuras arquitectónicas o en la
naturaleza. Proyectos como la construcción de modelos utilizando ángulos y
líneas pueden ayudarle a comprender cómo se relacionan los temas. Las
herramientas de modelado como Tinkercad pueden mejorar estas actividades al
permitirle crear diseños que incorporan líneas y ángulos.
Actividades
de refuerzo
1.
Juegos de identificación de ángulos: utilice juegos en línea como MathPlayground para ayudar a los estudiantes a practicar la identificación y
clasificación de ángulos en un entorno lúdico.
2.
Experimento de medición de ángulos: los estudiantes pueden medir ángulos en el
aula, en el patio de recreo o en casa usando un transportador para registrar
sus observaciones.
3.
Creación de formas geométricas: Organice actividades donde los estudiantes
creen formas usando líneas y ángulos, reforzando la aplicación práctica de
estos conceptos.
Evaluación
y retroalimentación
Evalúe
su comprensión con pruebas interactivas y tareas de práctica. Implemente
herramientas de evaluación en línea como Google Forms para recopilar las
respuestas de los estudiantes y brindar comentarios inmediatos. La evaluación
formativa le permite adaptar sus estrategias de enseñanza para satisfacer las
necesidades de sus estudiantes.
Estos enfoques y herramientas pueden proporcionar a los estudiantes una comprensión profunda de los ángulos y las líneas, permitiéndoles no solo aprender estos conceptos sino también aplicarlos de manera efectiva en una variedad de situaciones. Trabajemos juntos para hacer que la geometría sea accesible, interesante y relevante para todos.
Propuesta de sucuencia para Rectas y ángulos.
Secuencia Didáctica: Ángulos en
Primero de Secundaria
Tema: Ángulos
Nivel: Primero de
Secundaria
Duración: 5 sesiones (1
sesión por actividad)
Recursos:
- Tarjetas de bingo con conceptos básicos, marcadores,
papel bond, rotuladores de colores, pizarra, transportadores, papel bond cuadriculado.
Objetivos Generales:
- Identificar y clasificar diferentes tipos de
ángulos.
- Aplicar el conocimiento de ángulos para resolver
problemas complejos.
- Utilizar herramientas y materiales para construir y
medir ángulos.
- Evaluar el entendimiento del tema a través de una
actividad práctica.
1. Reactivación de Conocimientos
Propósito: Recordar
conceptos básicos que tienen relación con los ángulos.
Actividad: "Lluvia
de Ideas y Bingo de Conceptos"
- Lluvia de Ideas: Iniciar con una lluvia de
ideas en la que los estudiantes mencionen todos los conceptos matemáticos
que recuerdan de grados, líneas, vértices, y formas geométricas.
- Bingo de Conceptos: Crear
tarjetas de bingo con palabras clave relacionadas con ángulos y geometría
básica (como línea recta, vértice, grado, círculo, etc.). A medida que se
mencionan estos términos durante la discusión, los estudiantes marcarán
las palabras en sus tarjetas. El primero en completar una línea de bingo
gana un pequeño premio.
2. Construcción de Significados
Propósito: Proporcionar
nueva información sobre el tema de ángulos.
Actividad:
"Exploración de Ángulos"
- Explicación Teórica: Explicar
a los estudiantes los diferentes tipos de ángulos: agudo, recto, obtuso,
llano y completo. Utilizar gráficos y diagramas en la pizarra.
- Demostración Práctica: Utilizar
un transportador y un papel cuadriculado para mostrar cómo se mide cada
tipo de ángulo. Invitar a los estudiantes a medir ángulos en sus
cuadernos.
- Discusión en Clase: Discutir
las aplicaciones de los ángulos en la vida cotidiana, como en
arquitectura, diseño y navegación.
3. Organización del Conocimiento
Propósito: Organizar y
estructurar la información aprendida sobre ángulos.
Actividad: "Cuadro
comparativo de Ángulos"
- Instrucciones: Pedir al estudiante que
organicen la información sobre los ángulos a manera de cuadro comparativo.
- Contenido del cuadro: Los cuadros
deben incluir tipos de ángulos, propiedades, cómo se miden y un dibujo de
cada tipo.
4. Aplicación de Conocimientos
Propósito: Aplicar el
conocimiento adquirido sobre ángulos en situaciones prácticas.
Actividad:
"Construcción y Medición de Ángulos"
- Desafío: ¿Qué tipo de ángulo se muestra en cada uno de los siguientes diagramas?a)
 b)
b) C)
C) d)
d) mi)
mi) F)
F)
- Retroalimentación: Discutir en grupo cómo
llegaron a sus soluciones y qué errores, si los hubo, cometieron en el
proceso.
5. Problema Complejo y Evaluación
Propósito: Resolver un
problema complejo utilizando el conocimiento adquirido y evaluar el
entendimiento general del tema.
Actividad:
"Proyecto de Diseño: Parque de Diversiones"
- Contexto: Pedir a los estudiantes que diseñen un plano para
una nueva sección de un parque de diversiones que incluya varias
atracciones. Cada atracción debe incluir ángulos específicos (ej. la
entrada principal con un ángulo de 120°, la zona de juegos con ángulos de
90°, etc.).
- Planificación y Creación: Los
estudiantes trabajarán en grupos para planificar y dibujar su diseño,
asegurándose de medir y marcar claramente los ángulos en sus planos.
- Presentación: Cada grupo presentará su
diseño y explicará cómo utilizaron los ángulos en su proyecto.
- Evaluación: Evaluar los proyectos en base a la precisión de los
ángulos, la creatividad del diseño y la claridad de la presentación.